Вращательное движение – одна из основных форм движения в физике. Оно неразрывно связано с понятием о вращении объекта вокруг оси. Этот вид движения встречается в различных аспектах нашей жизни – от движения колеса автомобиля до вращения планет вокруг своих осей. Для понимания и изучения закона вращательного движения необходимо ознакомиться с его основными принципами и примерами в приложении к реальным ситуациям.
В центре понимания вращательного движения находится понятие момента силы. Момент силы определяется как произведение величины силы на ее плечо, то есть на расстояние от точки, вокруг которой происходит вращение, до линии действия силы. Чем больше момент силы, тем большее вращательное движение он вызывает.
Примером вращательного движения может служить вращение колеса велосипеда. Когда на колесо действует приложенная сила, оно начинает вращаться вокруг своей оси. Причем, если сила приложена далеко от оси вращения, момент силы будет большим, и колесо будет вращаться быстрее. Этот пример показывает, как закон вращательного движения проявляется в реальных ситуациях и влияет на поведение объектов в окружающем нас мире.
Основные принципы закона вращательного движения
Первым принципом является принцип сохранения момента импульса. Согласно этому принципу, момент импульса вращающегося тела остается постоянным, если на него не действуют внешние силы. Это означает, что вращательное движение может происходить без изменения скорости или направления.
Вторым принципом является принцип сохранения энергии. Согласно этому принципу, полная механическая энергия вращающегося тела остается постоянной, если на него не действуют внешние силы. Это означает, что энергия, присутствующая в системе тела и его вращения, не может появляться или исчезать, а только преобразовываться из одной формы в другую.
Третьим принципом является принцип сохранения массы. Согласно этому принципу, масса вращающегося тела остается неизменной, если на него не действуют внешние силы. Это означает, что масса тела не может увеличиваться или уменьшаться в процессе вращения.
Для более подробного описания и изучения вращательного движения, принципы закона вращательного движения могут использоваться вместе с другими физическими законами, такими как закон сохранения приращения момента импульса, закон сохранения углового момента и закон сохранения угловой скорости.
| Принцип | Описание |
|---|---|
| Принцип сохранения момента импульса | Момент импульса вращающегося тела остается постоянным без внешних сил. |
| Принцип сохранения энергии | Полная механическая энергия вращающегося тела остается постоянной без внешних сил. |
| Принцип сохранения массы | Масса вращающегося тела остается неизменной без внешних сил. |
Используя данные принципы, можно детально исследовать различные аспекты вращательного движения и применять их для решения разнообразных задач в физике и инженерии.
Угловая скорость и угловое ускорение
Угловая скорость обозначает скорость изменения угла поворота объекта и измеряется в радианах в секунду (рад/с). Угловая скорость определяется как отношение изменения угла (Δθ) к изменению времени (Δt):
ω = Δθ / Δt
Угловое ускорение, в свою очередь, является мерой изменения угловой скорости. Оно также измеряется в радианах в секунду в квадрате (рад/с²) и определяется как отношение изменения угловой скорости (Δω) к изменению времени (Δt):
α = Δω / Δt
Угловая скорость и угловое ускорение позволяют описывать движение вращающихся объектов и применяются во многих областях, включая физику, инженерию, астрономию и механику.
Примером применения угловой скорости и углового ускорения может служить движение планет вокруг Солнца. Угловая скорость планеты позволяет определить время, за которое она совершает один полный оборот вокруг Солнца, а угловое ускорение может использоваться для изучения изменения орбиты планеты под воздействием гравитационных сил.
а) Определение угловой скорости
Угловая скорость измеряется в радианах в секунду (рад/с) или в градусах в секунду (град/с). Она может быть постоянной или изменяться со временем в зависимости от условий вращения тела.
Этот параметр неразрывно связан с линейной скоростью тела и радусной скоростью. Угловая скорость является векторной величиной, которая имеет направление вдоль оси вращения тела.
Угловая скорость является важным физическим понятием для решения проблем вращательного движения, таких как определение момента инерции тела и углового ускорения.
Например, при рассмотрении вращения колеса автомобиля, угловая скорость определяет, насколько быстро колесо вращается вокруг своей оси. Она также позволяет определить угловое ускорение колеса при изменении скорости вращения.
Таким образом, понимание угловой скорости является ключевым для анализа и описания кинематических характеристик вращательного движения тел.
б) Расчет углового ускорения
Угловое ускорение (α) представляет собой изменение угловой скорости (ω) в единицу времени. Расчет углового ускорения может быть выполнен с использованием формулы:
| Формула | Значение |
|---|---|
| α = Δω / Δt | угловое ускорение (рад/с²) |
где Δω представляет собой изменение угловой скорости за определенный промежуток времени Δt. Значение углового ускорения может быть положительным, если угловая скорость увеличивается, и отрицательным, если угловая скорость уменьшается.
Расчет углового ускорения позволяет определить, насколько быстро изменяется угловая скорость вращающегося объекта. Это важный параметр при изучении вращательного движения и может быть использован для прогнозирования изменения угловой скорости в будущем.
Момент силы и момент инерции
Момент инерции, с другой стороны, измеряет сопротивление тела к изменению скорости вращения и определяется как сумма произведений массы каждой частицы тела на квадрат расстояния от оси вращения до данной частицы. Момент инерции зависит от распределения массы вокруг оси вращения и характеризует инертность тела относительно вращательного движения.
Одним из примеров, иллюстрирующих момент силы и момент инерции, является вращение тела под действием приложенной силы. Если тело имеет сосредоточенную массу и его ось вращения проходит через центр масс, момент инерции будет минимальным. Но если ось вращения располагается на некотором расстоянии от центра масс, момент инерции будет более значительным.
Важно понимать, что момент силы и момент инерции связаны между собой. Согласно закону движения вращательного тела, момент силы пропорционален скорости изменения момента инерции. Иными словами, чем больше момент инерции, тем сложнее изменить скорость вращения тела при одной и той же силе.
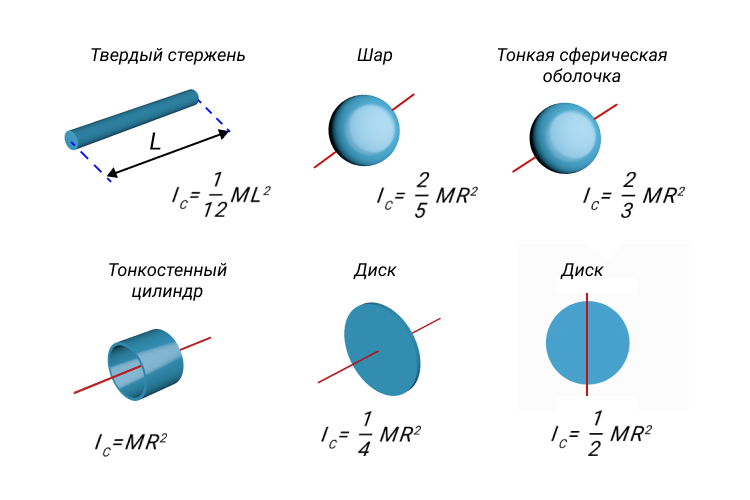
Таблица ниже показывает некоторые примеры момента инерции для различных геометрических фигур:
| Фигура | Момент инерции |
|---|---|
| Тонкое кольцо | I = mr² |
| Тонкий стержень (вокруг центра) | I = (1/12)ml² |
| Тонкий стержень (вокруг конца) | I = (1/3)ml² |
| Диск (вокруг центра) | I = (1/2)mr² |
| Сплошной сферический шар | I = (2/5)mr² |
Момент силы и момент инерции играют важную роль в понимании и анализе вращательного движения тел. Они позволяют определить, какие силы и какое распределение массы влияют на скорость вращения объекта.
а) Понятие момента силы
Момент силы обычно обозначается буквой M и измеряется в ньютон-метрах (Н·м). Ось вращения может быть любой, но при расчетах принято выбирать ось, вокруг которой происходит наименьший момент силы для упрощения вычислений.
Момент силы зависит от величины силы и расстояния от оси вращения до точки приложения силы. Чем больше сила и дальше точка приложения от оси, тем больше момент силы.
Примерами момента силы могут быть вращение руля автомобиля для изменения направления движения, крутящий момент, создаваемый двигателем автомобиля, и сила тяжести, приводящая к вращению земли вокруг своей оси.
б) Расчет момента инерции
Момент инерции вычисляется по формуле:
$$I = \sum m_i r_i^2$$
где:
- $$I$$ — момент инерции,
- $$m_i$$ — масса i-го элемента тела,
- $$r_i$$ — расстояние от i-го элемента тела до оси вращения.
Для простых геометрических фигур симметрии можно использовать аналитические формулы для расчета момента инерции. Например, для однородного прямоугольного тела, вращающегося вокруг оси, проходящей через его центр масс, момент инерции высчитывается по формуле:
$$I = \frac{1}{12} m (a^2 + b^2)$$
где:
- $$I$$ — момент инерции,
- $$m$$ — масса тела,
- $$a$$ и $$b$$ — размеры сторон прямоугольного тела.
Для более сложных фигур, таких как цилиндры, сферы или конусы, момент инерции вычисляется с использованием интеграла или табличных данных. Точные аналитические формулы зависят от формы и ориентации тела относительно оси вращения.
Расчет момента инерции является важным этапом при изучении вращательного движения и позволяет анализировать его свойства и влияние на поведение тела в пространстве.
Закон сохранения момента импульса
Момент импульса определяется как произведение массы тела на его угловую скорость и его момент инерции:
$$L = I \cdot \omega$$
где:
- L — момент импульса;
- I — момент инерции тела;
- ω — угловая скорость.
Согласно закону сохранения момента импульса, если на замкнутую систему, состоящую из нескольких взаимодействующих тел, не действуют внешние моменты сил, то сумма моментов импульса всех тел системы должна оставаться постоянной. Другими словами, если одно тело системы начинает вращаться быстрее, то другое тело должно начать вращаться медленнее, чтобы сохранить общий момент импульса системы.
Закон сохранения момента импульса находит широкое применение в различных областях физики, включая механику, аэродинамику, астрономию и многие другие. Он помогает объяснить множество явлений, связанных с вращательным движением, и является важным инструментом для анализа и моделирования таких систем.
| Примеры применения закона сохранения момента импульса: |
|---|
| Вращение планет вокруг Солнца |
| Вращение волчка |
| Вращение ротора электромотора |
| Спутниковые системы и космические станции |
| Движение велосипедиста на велосипеде |
Вопрос-ответ:
Какие основные принципы закона движения вращательного движения?
Основные принципы закона движения вращательного движения включают принцип сохранения момента импульса, принцип сохранения энергии и принцип сохранения углового момента.
Что такое момент импульса в вращательном движении?
Момент импульса в вращательном движении — это величина, которая характеризует количество движения вращающегося объекта. Он определяется произведением массы объекта на его угловую скорость и радиус вращения.
Как применяется закон движения вращательного движения в практических примерах?
Закон движения вращательного движения применяется во многих практических примерах, таких как движение планет вокруг Солнца, вращение колес автомобиля, движение ветряных мельниц и т.д. Он позволяет определить угловую скорость, момент силы, момент инерции и другие параметры вращающихся объектов.
Какие еще физические законы связаны с вращательным движением?
Помимо закона движения вращательного движения, с вращательным движением связаны такие физические законы, как закон сохранения энергии, закон сохранения углового момента и закон сохранения момента импульса.
Какие единицы измерения используются при изучении вращательного движения?
При изучении вращательного движения используются следующие единицы измерения: радианы для измерения углов, метры для измерения радиуса, секунды для измерения времени, килограммы для измерения массы и другие.
Какой закон движения применяется к вращательному движению?
К вращательному движению применяется закон сохранения момента импульса. Этот закон гласит, что если на тело не действуют моменты сил, то момент импульса тела остается постоянным. То есть, если нет внешнего воздействия, то тело будет вращаться с постоянной угловой скоростью.